Un degré de complexité géométrique intraseque dans la vie courants.:

• Les réflexions selon une droite (dans le plan ou l'espace) ou selon un plan (dans l'espace),
• les symétries centrales,
• les translations,
• les rotations de centre C (dans le plan) ou d'axe (D) dans l'espace,

Les réflexions, symétries, translations, rotations sont des exemples d'isométries du plan ou de l'espace. Certaines conservent les angles orientés et sont alors appelées des déplacements. L'ensemble des déplacements forme un groupe.

• les homothéties,

Les homothéties et les isométries sont des exemples de similitudes du plan ou de l'espace. On démontre même que ces transformations engendrent l'ensemble des similitudes. Les similitudes conservant les angles orientés forment un groupe appelé le groupe des similitudes directes.

• les affinités.

Les affinités et les similitudes sont des exemples de transformations affines du plan ou de l'espace. On démontre même que ces transformations engendrent l'ensemble des transformations affines.

Il existe aussi des transformations qui ne sont pas définies dans le plan ou l'espace tout entier. Parmi celles-ci on peut citer les inversions, les homologies qui sont des transformations homographiques

ces classes contient la précédente.

• les inversions, conservant l'ensemble des droites et des cercles dans le cas plan, ou transformations de Moebius, conservant l'ensemble des plans et des sphères, en dimension 3.

image de départ	isométrie	similitude

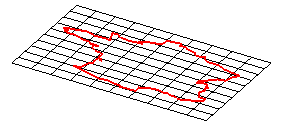
transformation affine	transformation homographique	inversions

• les transformations bidifférentiables ou difféomorphismes sont les transformations qui sont affines au premier ordre ; elles contiennent les précédentes comme cas particuliers, mais aussi :

• les transformations conformes ou anticonformes, conservant les angles, qui sont, au premier ordre, des similitudes

• les transformations équivalentes ou équiaréales, conservant les aires dans le cas plan, ou les volumes dans le cas 3D, qui sont, au premier ordre, des transformations affines de déterminant 1

Et enfin, englobant les précédentes :

• les transformations bicontinues ou homéomorphismes, conservant les voisinages des points

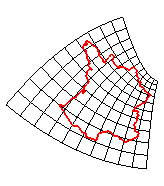
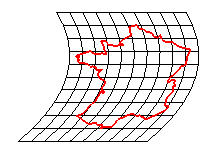
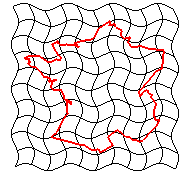
Transformation conforme	transformation équivalente	Difféomorphisme	Homéomorphisme

On crée alors des groupes et des sous-groupes de transformations.

L'étude de la géométrie est en grande partie l'étude de ces transformations.